Digital audio is a representation of sound in digital form by means of modulation for the purpose of processing, storage and transmission. While there are a number of different digital modulation methods (e.g. Pulse Density Modulation (PDM), Pulse Position Modulation (PPM), Pulse Amplitude Modulation (PAM), Pulse Number Modulation (PNM)), by far the most widely used in the audio field is Pulse Code Modulation (PCM).
A. PULS CODE MODULATION (PCM)
The technology of PCM was developed in 1937 by the British scientist Alec Reeves for telecommunications applications. But it was not commercially viable at the time based on the then current tube technology. It was only after the introduction of transistor technology that the BBC in England and Nippon Columbia in Japan began developing commercial PCM sound recording devices in the late 1960s. Denon (a subsidiary of Nippon Columbia) began releasing the first commercial digital music albums in 1971 (Steve Marcus: “Something”, January 1971), albeit still on analogue vinyl. The introduction of the compact disc (CD) as a sound carrier did not take place until 1981 at the Berlin Funkausstellung by Sony/Philips. In the USA, Soundstream and 3M followed in the mid-1970s with their own PCM recorders.
I. Basics of PCM
In order to digitise (convert into discrete numbers) analogue (continuous) audio data, analogue-to-digital converters (ADC) convert the analogue audio signal into 2 discrete characteristics:
Sampling rate
refers to the frequency with which the continuous-time audio signal (grey line in graph 1) is sampled (i.e. samples are taken) in a given time interval and converted into a discrete-time signal (red arrows in graph 1) – e.g. in the Red Book Standard of the CD 44,100 times per second. Usually, the analogue signal is time-constantly sampled by pulse amplitude modulation, i.e. always at equal time intervals of e.g. with the Red Book Standard every 1s/44,100=22.67 µs.

Graph 1: Sampling of an analogue signal
In compliance with the Nyquist-Shannon sampling theorem, frequencies up to half the sampling rate (½fS) can be encoded and reconstructed without loss, so that the waveform reconstructed from the digital data corresponds exactly to the original analogue waveform. Digitisation influences neither the frequency response nor the phase response. However, the theorem assumes ideal anti-aliasing and reconstruction filters(sinc filter). The sampling rate is thus a measure of the temporal resolution of the audio signal and determines the frequency range. The following maximum frequency ranges result for common sampling rates:
| Sampling rate | Frequency range |
| 44.1kHz | 1Hz – 22.05kHz |
| 88.2kHz | 1Hz – 44.1kHz |
| 96.0kHz | 1Hz – 48.0kHz |
| 192.0kHz | 1Hz – 96.0kHz |
Word length
also bit depth refers to the values of the measuring points at each of the sampling points (red arrows in diagram 1) with which the continuous-value amplitude of the audio signal is converted into a discrete-value signal (quantisation). After encoding, it indicates the amplitude of the continuous signal at this point in time in bits (red steps in graphic 2) and thus determines the dynamic resolution (dynamic range) of the digitisation at this point in time. The number of quantisation steps is determined with 2n, where n represents the word length.

Graph 2: Quantisation of an analogue signal
In the Red Book Standard of the CD, for example, the amplitude at the time of measurement is resolved with a maximum of 16 bits, i.e. 16 digits consisting of zeros and ones. Accordingly, these 16 bits allow 216 =65,536 different degrees of amplitude or volume levels of the sound signal. Since 1 bit corresponds to approx. 6 dB of dynamic range, this results in a maximum dynamic range of approx. 96 dB for 16 bits. The values for other common word lengths are:
| Bit depth | Max. amplitude values | Dynamic range |
| 8 Bit | 28 = 256 | 48 dB |
| 16 Bit | 216 = 65.536 | 96 dB |
| 24 Bit | 224 = 16.777.216 | 144 dB |
| 32 Bit | 232 = 4.294.967.296 | 192 dB |
It should be noted here that regardless of the values in the table, the effective dynamic range for each word length can be extended by dithering and noise shaping. For example, it is possible to extend the effective dynamic range of 16-bit recordings to approx. 100 – 120dB by adding a specially distributed dithering signal to the signal, which has a reduced amplitude in the mid-range and a correspondingly increased amplitude in the highs and lows. In this way, the noise in the mid-range, which is particularly sensitive to the human ear, can be reduced and subjectively higher noise margins can be achieved with a constant dither level. Conversely, it should also be mentioned that real 24Bit or beyond can hardly be realised with today’s electronic components. The reason for this is the thermal noise of the electronic components used (Johnson noise), especially the resistors, at room temperature, which is somewhat above -140 dB.
In summary: the sampling rate represents the timing of the measurement and the word length represents the values of the measurement of the analogue audio signal in the digitisation process.
II. Quantisation errors and dithering
Since quantisation uses a fixed grid (e.g., 16, 24 or 32 bits), the quantisation process is inherently error-prone: Actual amplitude values have to be rounded up or down to the nearest grid value. With a continuous analogue signal (grey line in graph 3), most of the amplitude values at the measuring points (grey dots in graph 3) are not identical to the quantised amplitude values (values 1-7) of the X[t] axis), but lie somewhere between two amplitude values. These are rounded up or down to the nearest amplitude value. This difference between the actual analogue value and the quantised amplitude value results in so-called quantisation errors, which can be a maximum of ½ of the quantisation interval or Least Significant Bit (LSB). A sequence of quantization errors is modelled as an additive random signal, like white noise, called quantization noise because of its stochastic behaviour. This means that when the digital files are played back, some measuring points are played back somewhat louder than the original and others somewhat quieter. Increasing the number of rasters (i.e., bit depth) reduces the problem by decreasing the quantisation intervals, but it can never eliminate it completely. Each extra bit doubles the number of quantisation intervals: 16bit has 216 =65,536 intervals or volume steps, 17bit has 217 =131,072 intervals etc.. Accordingly, with each extra bit, the size of the intervals and thus the quantisation errors are halved, which is noticeable in a reduction of the noise floor by about 6dB per extra bit.

Graph 3: Quantisation error
At high signal levels, the size of the quantisation error will be distributed with equal probability between the limits ± ½LSB, so that the quantisation errors are randomly distributed and thus act like uncorrelated white noise – i.e. little disturbing. Towards low signal levels, however, they become very large in relation to the quantised signal and cease to be randomly distributed, so that at low signal levels they lead to noticeable and disturbing “granular noise” (a kind of non-linear distortion). Whereas with the “old” analogue technology distortion increases with increasing amplitude levels, with digital technology it is exactly the other way round: just levels lead to unpleasant audible distortions. To make these artefacts inaudible, so-called dithering is performed: noise with certain statistical properties is added to the analogue signal before quantisation in order to smooth the stair-step-like transfer function that occurs at low levels. On the one hand, this increases the overall noise level and reduces signal-to-noise ratio (SNR). On the other hand, by adding dither noise, the quantisation error takes on a white-noise-like and signal-independent character. Dithering has the task of transforming the quantisation error occurring at low levels, which represents a distortion correlated with the music signal, into a white noise independent of the music signal. Dithering does not mask the quantisation error, but allows the ADC to encode amplitudes smaller than the LSB. As a result, the digital signal behaves like an analogue signal – it does not become increasingly distorted as it gets quieter, but remains faithful and clean until it disappears under the noise floor.
Besides the quantisation error, other errors can also occur during quantisation, e.g. zero point error (offset), gain error, non-linearity error, step error and the much-discussed clock jitter (fluctuations in the period of the clock signal), which lead to a deviation of the reconstructed digital signal from the original analogue signal.
III. Is information lost in the process of digitization?
The question that immediately arises is whether information is lost between the measuring points when digitising (sampling & quantising), so that the digital reproduction of the analogue sound signal is inherently incomplete and thus inferior. The answer is – surprisingly – no. At least with the correct application of the sampling theorem, no information is lost. The waveform reconstructed from the digital data is exactly the same as the original analogue waveform. Digitisation influences neither the frequency response nor the phase behaviour.
It is true that the set of measurement points (grey dots in graph 4) results in a multitude of alternative possible frequency courses (e.g. dashed line in the following graph), which all completely cover the set of measurement points. However, all but one have a frequency higher than the Nyquist frequency. By using a low-pass filter that filters out all frequencies above the Nyquist frequency, it can be ensured that only the frequency response – out of all possible frequency responses that cover all measuring points – that corresponds exactly to the original analogue frequency response is transmitted.

Graph 4: Alternative frequency responses for all measuring points
In other words, since the original frequency response is the one with the highest possible frequency that still covers all points, the Nyquist-Shannon sampling theorem guarantees that after applying the reconstruction filter, the reconstructed frequency response cannot deviate from the original frequency response.
For the example of the Red Book Standard, this means that with the sampling rate of 44.1kHz used, sound signals up to 22,050Hz can be digitised without loss. Since the human ear can only perceive sound from approx. 20Hz to 20,000Hz, digitisation according to the Red Book Standard should be sufficient for all audio applications, at least as far as the sampling rate is concerned. The fact that it is not quite sufficient in practice, because the available filters required in the conversion process are not sufficiently steep enough (cutting off sharply at a certain frequency) to attenuate the signal sufficiently in the range between 20,000Hz and 22,050Hz without damaging the frequency ranges in the audible band below, will be discussed further down.
However, this does not mean that correct digitisation is a lossless process. This is because the choice of word length is arbitrary and in any case lossy. A quantised digital signal cannot reproduce a continuous amplitude curve without loss, regardless of the word length. However, there is a point at which psychoacoustically, differences in the dynamic gradation are no longer perceptible. Exactly where this point lies is the subject of various research efforts. In general, it is assumed that the amplitude resolution of the human ear allows for more than 1 million gradations, so that it can still distinguish volume differences of 0.0001dB in the center of the human hearing area, which would roughly correspond to the order of magnitude of a 20-22bit digital system.
IV. Nyquist-Shannon sampling theoren and aliasing
Following the Nyquist-Shannon sampling theorem, a complete (i.e. loss-free) mapping of a band-limited signal at a temporally constant sampling rate with the upper cut-off frequency fN (also called Nyquist frequency) can be achieved by a sampling rate fS that is at least twice as high:
fS > 2xfN
A periodic, discrete sampling of the signal in the time domain results in an equally periodic, discrete spectrum in the frequency domain. So-called aliasing effects occur, i.e. ultrasonic reflections of the original analogue signal at multiples of the sampling rate (fS) with decreasing amplitude:

Graph 5: Aliasing effects of a frequency fout
If the Nyquist-Shannon sampling theorem is violated by sampling components of the useful frequency band higher than fS/2, so-called aliasing errors occur. I.e. overlapping of the mirror spectra with the consequence that even in the audible range interference signals are superimposed from the next higher mirroring and become noticeable as disturbances and distortions, so that the reconstructed sound signal no longer corresponds to the original analogue signal:

Graph 6: Aliasing error when fN > ½fS
Therefore, the band-limiting condition is important. By means of an analogue low-pass filter (filter that passes all frequencies below a certain frequency and blocks all above) to limit the input frequency fN , the signal is band-limited so that sampling errors are avoided. Such a filter should be as steep as possible and have a high attenuation, e.g. in the Red Book standard the filter must drop -96dB between 20.0kHz and 22.05kHz – which is difficult to achieve even with the most elaborate filters of higher (eighth or higher) order. Nevertheless, with analogue filters, parts of the signal below the Nyquist frequency are inevitably attenuated and parts above the Nyquist frequency are not completely eliminated:
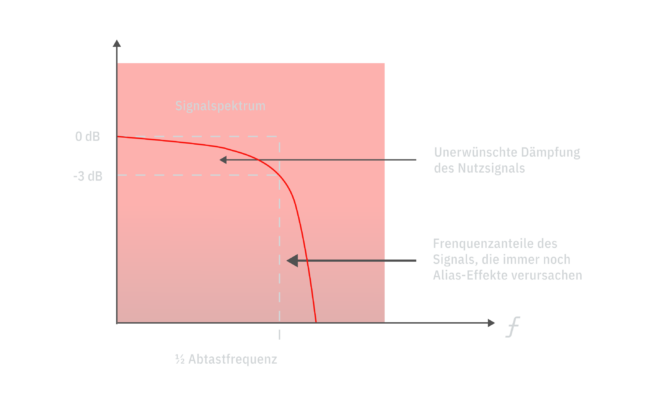
Graph 7: Inadequacy of analogue filters
The exact choice of the cut-off frequency for the filter is therefore a compromise between the preservation of the useful signal and the elimination of aliasing errors. On top of that, the filter itself causes a number of distortions and problems in the useful signal (e.g. ringing, group delay, phase distortions, etc.), so that nowadays, instead of analogue anti-alias filters, the input signal is generally sampled with a multiple of the sampling frequency (oversampling) and then digitally filtered. This creates a larger safety margin between the useful frequency band and the alias spectrum, which significantly reduces the demands on the filter. In addition, filters in the digital domain, although mathematically demanding in design, are easy to realise.
V. Oversampling and upsampling
In digital signal processing, one speaks of oversampling when a signal is sampled with a higher sampling rate (usually integer multiples) than is actually required for the representation of the signal bandwidth (according to the Nyquist-Shannon theorem). This is common practice in most A/D or D/A converters to improve their operations. Upsampling is a sample rate conversion of a digital signal. Both operations are mathematically similar; only the application case differs. Upsampling is achieved by interpolating existing samples with copies of the existing samples: e.g. when upsampling a CD (with a sampling rate of 44.1kHz) 4 times, 3 copies of each existing sample are added for each sample, thus increasing the sampling rate from 44.1kHz to 176.4kHz. Although the additional samples do not contain any new or different information, they ensure that the aliasing spectra begin at a significantly greater distance from the audible frequency range. In both cases of oversampling or upsampling this allows the use of mild anti-aliasing filters that have less of a negative influence on the music signal, because they have a much wider frequency range available for their operation and can therefore be softer (second or third order filters). As explained, it is technically very difficult to meet the requirements for anti-aliasing filters in the analogue domain. In the digital domain, on the other hand, it is relatively easy with FIR filters (Finite Impulse Response filters), that are also less problematic in terms of phase behaviour and group delays than corresponding analogue filters. Over- and upsampling thus allows the filtering of the signal to be shifted from the analogue to the digital domain, thereby improving the signal-to-noise ratio and avoiding aliasing and phase distortion. The filtering is done with a digital filter; only a relatively simple analogue reconstruction filter is then necessary at the converter output.

Graph 8: Oversampling extends the working range of the anti-aliasing filters
However, the realisation of a digital anti-aliasing filter as a prerequisite for digitisation is conceptually challenging, since it presupposes that the signal is already digitised. The solution is a clever engineering achievement using oversampling:
Let’s take 2-fold oversampling as an example:
- With 2-fold oversampling, on the analogue-to-digital conversion side, the analogue audio signal is first limited to e.g. 1.5fS by a mild analogue low-pass filter. This allows the filter range to be extended to 0.5fS – 1.5fS. Using the Red Book standard as an example, this corresponds to an expansion of the frequency band for filtering by a factor of 20 from 2.05kHz to 44.1kHz. Subsequently, the signal is quantised with twice the sampling rate and converted by a digital low-pass filter with subsequent decimation of the sampling points by 2-fold undersampling to the digital signal without aliasing errors with the desired sampling rate f
- With 2-fold oversampling, the digital signal is doubled on the digital-to-analogue conversion side by means of sampling rate conversion and a digital low-pass filter before it is converted to analogue and finally reconstructed error-free with an analogue low-pass filter according to the Nyquist-Shannon theorem.
The multiplier for the oversampling operation can range from 2x, 4x or 8x up to 64x, 128x (5.6 MHz sampling rate) or more for DSD productions.
A positive side effect is that oversampling improves the signal-to-noise ratio. The previously mentioned broadband quantisation noise at higher levels, which is uncorrelated with the input signal, is distributed over a wider spectrum and gets pushed out to the new Nyquist frequency kfS/2. Consequently, less noise power exists in the usable audio band. Within the same bandwidth, the noise level decreases by 3dB for each doubling of the sampling frequency

Graph 9: Shift in quantisation noise due to oversampling
The digital filters, however, lead to a new phenomenon: pre-ringing. Pre-ringing describes the phenomenon, where the impulse response exhibits – in addition to the post-oscillation (which also occurs with analogue filters) – also an unnatural pre-oscillation (pre-ringing) before the entry of the actual signal, so that the filter “smears” the signal over time. In the following graphs 10 & 11, the original pulse with a width of 1 sample is smeared in time by the filter over many samples. This phenomenon is mainly responsible for the sometimes unnatural sound quality of digital recordings (hard sound textures, lack of spatiality, high frequencies that sound flat and brilliant at the same time, etc.):

Graph 10: Original pulse of 1 sample

Graph 11: Pulse after application of linear phase filter
Pre-ringing occurs with the steep-edged anti-aliasing filters of AD converters as well as with the usual steep-edged, linear-phase reconstruction filters of DA conversion, primarily at low sampling rates such as 44.1 kHz or 48.0 kHz. However, the extent to which filter ringing actually affects playback quality is controversial. Ringing generally occurs between the passband and the stopband of a filter, in the example of a CD, between 20kHz and 22.05kHz, at higher sample rates at correspondingly higher frequencies. Pre-ringing, which is most pronounced with linear-phase filters, can be mitigated by alternative filter topologies (minimum-phase, apodising, etc.). However, these alternative filters are always a compromise, as they bring disadvantages in other areas, such as phase distortion or treble drop. The phenomenon can be largely avoided by higher sampling rates and smoother filter gradients.
Oversampling, by the way, does not lead to higher data rates and higher memory consumption, as this process takes place when data is read out and not when it is written.
VI. Digitalisation process (Sigma delta process)
With the basic knowledge so far covered, we can now look at the process steps in digitisation:
The technical realisation of analogue-to-digital converters in today’s digital audio technology mainly takes place through the sigma-delta method. Taking the idea of oversampling further, 64 times the standard sampling frequency is used (64×44.1 kHz = 2.8224 MHz), but originally only with one bit word length. A sigma-delta converter (ΣΔ-converter, see graph 12) basically consists of two stages, an analogue modulator and a digital filter. The analogue modulator is basically composed of a series-connected input differential amplifier, an integrator (Σ) and a comparator (Δ), which functions as a 1-bit quantiser, and a one-bit D/A converter in the negative feedback branch. With the help of the following digital FIR filter, which decimates the sampling rate and functions in principle like an averaging accumulator (for the samples), the digital output word is generated with the desired sampling frequency and word length.
The basic operation is best demonstrated using a first-order sigma-delta converter (the order is determined by the number of low-pass filters or integrators before the comparator):

Graph 12: Basic structure of a sigma-delta converter
The input differential amplifier subtracts the negative feedback output signal of the 1-bit D/A converter from the input signal, to be measured at point V1. This is added to its previous output signal in the integrator (measuring point V2) and then compared with a voltage of 0V in the comparator. If V2 is greater than 0V, it assumes a voltage value of +1V at the output ( = V3); if it is less than 0V, it sets the output to -1V. In the negative feedback branch, the clocked one-bit D/A converter switches to + or -1V according to the measuring point V3 and passes this value on to the input differential amplifier, where it is in turn subtracted from the possibly changed input signal VIn that is now present. This cycle repeats itself per sampling rate.
However, the signal at the output of the modulator of a simple one-bit-ΣΔ converter contains an extremely high amount of quantisation noise. The resulting signal-to-noise ratio is so poor (6dB) – although the noise power is distributed up to the Nyquist frequency at 1.4112 MHz – that one can only achieve the desired dynamic range by spectral shaping in the so-called noise-shaping process. In this process, the statistically white noise in the spectrum is shifted as far as possible out of the audio band (20Hz – 20kHz). Although the sum of the total noise is not reduced, the amount of noise reduced in the audio band increases the amount of noise in the remaining range. Noise shaping is achieved by feeding the quantisation errors that lead to the quantisation noise back into the differential amplifier through a feedback loop from the 1-bit D/A converter with a time shift of 1 sample and a negative sign. Since each feedback loop acts as a filter, the error itself can be filtered by feeding back the error signal. The deformation of the quantisation noise already takes place in the integrator, thus in the analogue range. If the integrator is realised as an analogue low-pass filter, the result is an output signal that consists of the sum of the low-pass filtered input signal and the high-pass filtered noise. Thus, on the one hand it fulfils the anti-aliasing filtering, but on the other hand it also fulfils the spectral deformation of the quantisation noise.
The subsequent digital decimation filter, like the integrator, performs two tasks: on the one hand, the quantisation noise is filtered out along with all audio components above half the sampling frequency, so that under-sampling to the desired sampling frequency is possible (sampling theorem); on the other hand, the FIR filter serves to generate the required word length of the output signal. This is done by combining several delayed 1-bit samples into an n -bit sample. The word length that can be achieved in this way is not dependent on the dynamics of the sigma-delta modulator, but on the filter function
On the D/A side, the ΣΔ-converter is used again. For this purpose, the audio signal is first oversampled to usually 8 times the standard sampling rate (oversampling with the help of an interpolation filter), after the ΣΔ-converter the one-bit stream signal is available again. Finally, an internal switched capacitor filter (S.C.F. lowpass) pre-filters it in analogue form.
In summary, the PCM A/D and D/A conversion process and use of the sigma-delta method looks like this, whereby the use of a 1-bit converter described above for reasons of simplicity has been replaced by a multi-bit converter (mostly 4 or 8 bits), as is common today:

Graph 13: Modern PCM AD and DA conversion process
First, the A/D conversion takes place at a high sampling rate using a sigma-delta converter. Then, by decimation with a digital FIR filter, the desired quantisation can be achieved at the appropriate sampling frequency. After the recording process, an interpolation (oversampling) with quite steep-edged filters and renewed sigma-delta conversion is required for the D/A conversion before the signal is available again as an analogue output signal through low-pass filtering.
B. DIRECT STREAM DIGITAL (DSD)
This is where the idea of Direct Stream Digital (DSD) technology comes in, which was developed by Philips in the late 1990s for archiving purposes: If the decimation filter, the oversampling filter and the sigma-delta modulator were simply omitted, and the one-bit data signal were recorded directly and sent to the analogue low-pass filters on the D/A converter side, it would not only be possible to save some components, but above all to avoid the steep-edged anti-aliasing filters (and the associated pre-ringing). Even if the storage of the unfiltered DSD data stream requires more channel capacity than necessary, the omission naturally means a visible simplification. The end result is Pulse Density Modulation (PDM), which no longer quantifies the amplitude of the signal, but only the difference in amplitude from the previous sample:

Graph 14: Modern 1Bit DSD AD and DA conversion process
As a general rule in audio, the simpler an electrical circuit is and the less it interferes with the analogue signal to be transported, the higher the fidelity of the signal, so that ceteris paribus, simpler systems are preferable.
The technical development of A/D and D/A converters as multi-bit converters puts this apparent advantage of DSD technology into perspective. The advantages of low-cost production and very good linearity of sigma-delta converters are offset by the significantly lower dynamic range on both the A/D and D/A sides. The desire to increase the signal-to-noise ratio could only be fulfilled by varying the converters: fast 4- or 5-bit converters were used instead of the simple comparators, which meant that the necessary noise shaping could be made less severe. To avoid differential non-linearities as much as possible, several of these converters are used in the ICs, each of which receives the signal at random. The error resulting from the non-linearity of a single converter is smoothed out and becomes noticeable as noise.
This means that the one-bit signal required for DSD no longer appears in the signal flow of today’s digital productions, since a multi-bit signal is now available as the native format after the sigma-delta modulator. In order to obtain the one-bit signal from the (already digitised) output signal of the modulator, a downstream digital one-bit quantiser is required. This necessary stage, of course, again involves adding additional distortion and additional noise. On the D/A side, it is necessary to calculate the 4- to 5-bit modulator input word by low-pass filtering, but this can be done without distortion. The digital pre-filtering is even quite favourable, since high-frequency interference power is already eliminated here.
This results in the following process schematics for DSD recording with the aid of multibit sigma-delta converters, common today:

Graph 15: Modern DSD AD and DA conversion process
© Alexej C. Ogorek
Sources:
- Ken C. Pohlmann: “Principles of Digital Audio”, 6th Edition, McGraw-Hill 2011
- HUGH ROBJOHNS: ” All About Digital Audio”, Sound-On-Sound, May 1998
- Dominik Blech, Min-Chi Yang: “Untersuchung zur auditiven Differenzierbarkeit digitaler Aufzeichnungsverfahren”, Hochschule für Musik Detmold, Erich-Thienhaus-Institut 2004

