Digital Audio ist eine Modulationsmethode für Tonsignale zum Zwecke der Verarbeitung, Speicherung und Übertragung. Zwar gibt es eine Reihe verschiedener digitaler Modulationsmethoden (z.B. Pulse-Density-Modulation (PDM), Pulse-Position-Modulation (PPM), Pulse-Amplitude-Modulation (PAM), Pulse-Number-Modulation (PNM)), doch die mit Abstand am weitesten verbreitete ist Puls Code Modulation (PCM).
A. PULS CODE MODULATION (PCM)
Die PCM-Technologie wurde 1937 von dem britischen Wissenschaftler Alec Reeves für Telekommunikationsanwendungen entwickelt, war aber in der damaligen Zeit auf Basis der damaligen Röhrentechnologie nicht kommerziell verwertbar. Erst nach Einführung der Transistortechnik begannen die BBC in England und Nippon Columbia in Japan mit der Entwicklung kommerzieller PCM-Tonaufzeichnungstechnologien in den späten 1960ern. Denon (eine Tochter von Nippon Columbia) begann mit der Veröffentlichung der ersten kommerziellen Digitalmusikalben in 1971 (Steve Marcus: “Something”, Januar 1971), allerdings noch auf analogem Vinyl-Tonträger. Die Einführung der Compact Disk (CD) als Tonträger erfolgte erst 1981 auf der Berliner Funkausstellung durch Sony/Philips. In den USA folgten Mitte der 70er Jahre Soundstream und 3M mit eigenen PCM-Rekordern.
I. Grundlagen von PCM
Um analoge (kontinuierliche) Audiodaten zu digitalisieren (in diskrete Zahlen – Nullen und Einsen – zu wandeln) wandeln Analog-Digital-Konverter (ADC) das analoge Tonsignal in 2 diskrete Kenngrößen um:
Abtastrate
Auch Samplingrate, bezeichnet die Häufigkeit, mit der das zeitkontinuierliche Tonsignal (graue Linie in Graphik 1) abgetastet wird (d.h., Samples oder Proben entnommen werden) und in ein zeitdiskretes Signal umgewandelt wird (rote Pfeile in Graphik 1) – z.B. beim Red Book Standard der CD 44.100 mal pro Sekunde. Üblicherweise wird das analoge Signal per Pulsamplitudenmodulation zeitkonstant abgetastet, d.h. in immer gleichen zeitlichen Abständen von z.B. beim Red Book Standard alle 1s/44.100=22,67 µs.

Graphik 1: Sampling eines analogen Signals
Unter Einhaltung des Nyquist-Shannon-Abtasttheorems können Frequenzen bis zur halben Abtastrate (½fS) verlustfrei kodiert und wieder rekonstruiert werden, so dass die aus den digitalen Daten rekonstruierte Wellenform exakt der ursprünglichen analogen Wellenform entspricht. Die Digitalisierung beeinflusst weder den Frequenzverlauf noch das Phasenverhalten. Allerdings setzt das Theorem ideale Antialias- und Rekonstruktionsfilter voraus. Die Abtastrate ist somit ein Maß für die zeitliche Auflösung des Tonsignals und bestimmt den Frequenzumfang. Es ergeben sich folgende maximale Frequenzumfänge für übliche Abtastraten:
| Abtastrate | Frequenzumfang |
| 44,1kHz | 1Hz – 22,05kHz |
| 88,2kHz | 1Hz – 44,1kHz |
| 96kHz | 1Hz – 48,0kHz |
| 192kHz | 1Hz – 96,0kHz |
Wortbreite
Auch Bittiefe definiert die Größe der Messpunkte zu jedem der Abtastpunkte (rote Pfeile in Graphik 1) mit denen die wertkontinuierliche Amplitude des Tonsignals in ein wertdiskretes Signal umgewandelt wird (Quantisierung). Sie gibt, nach der Codierung, die Amplitude des kontinuierlichen Signals zu diesem Zeitpunkt in Bit an (rote Stufen in Graphik 2) und legen somit die dynamische Auflösung (Dynamikumfang) der Digitalisierung zu diesem Zeitpunkt fest. Die Anzahl der Quantisierungsstufen ermittelt sich mit 2n, wobei n die Wortbreite darstellt.

Graphik 2: Quantisierung eines analogen Signals
Beim Red Book Standard der CD z.B. wird die Amplitude zum Messzeitpunkt mit max. 16 Bit aufgelöst, d.s. 16 Ziffern bestehend aus Nullen und Einsen. Entsprechend erlauben diese 16 Bit 216=65.536 verschiedene Amplituden- oder Lautstärkegrade des Tonsignals. Da 1 Bit ca. 6 dB an Dynamikumfang entspricht, ergibt sich für 16 Bit ein maximaler Dynamikumfang von ca. 96 dB. Die Werte für andere übliche Wortbreiten sind:
| Bittiefe | Max. Amplitudenwerte | Dynamikbereich |
| 8 Bit | 2^8 = 256 | 48 dB |
| 16 Bit | 2^16 = 65.536 | 96 dB |
| 24 Bit | 2^24 = 16.777.216 | 144 dB |
| 32 Bit | 2^32 = 4.294.967.296 | 192 dB |
Es sei an dieser Stelle angemerkt, dass ungeachtet der Werte der Tabelle, der effektive Dynamikumfang für jede Wortbreite durch Dithering und Noise Shaping erweitert werden kann. So ist es z. B. möglich, den effektiven Dynamikumfang von 16Bit Aufnahmen auf ca. 100 – 120dB zu erweitern, indem dem Signal ein speziell verteiltes Dithering-Signal hinzugefügt wird, das im mittleren Tonbereich einen reduzierten und in den Höhen und Tiefen eine entsprechend verstärkte Amplitude aufweist. So kann, bei – in Summe, konstantem Dither-Level – das Rauschen in dem für das menschliche Gehör besonders empfindlichen Mittenbereich reduziert und subjektiv höhere Rauschabstände erreicht werden. Umgekehrt sei auch erwähnt, dass echte 24Bit oder darüber hinaus mit heutigen Technologien kaum zu realisieren sind. Der Grund hierfür liegt im thermischen Rauschen der verwendeten elektronischen Bauteile, insbesondere der Widerstände, bei Raumtemperatur, das sich etwas oberhalb von -140 dB abspielt.
Zusammenfassend: die Abtastrate repräsentiert die Zeitpunkte der Messung und die Wortbreite die Werte der Messung des analogen Tonsignals im Digitalisierungsprozess.
II. Quantisierungsfehler und Dithering
Da die Quantisierung mit einem fixen Raster (z.B., 16 oder 24Bit) erfolgt, ist der Quantisierungsprozess inhärent fehlerbehaftet. Bei einem kontinuierlichen analogen Signal (graue Linie in Graphik 3) sind die meisten Amplitudenwerte an den Messpunkten (rote Punkte in Graphik 3) nicht identisch mit den quantisierten Amplitudenwerten (Werte 1-7) der X[t]-Achse), sondern liegen irgendwo zwischen zwei Amplitudenwerten. Diese werden zum nächst-gelegenen Amplitudenwert auf- oder abgerundet. Aus dieser Differenz des tatsächlichen analogen Wertes und dem zugerechneten quantisierten Amplitudenwert ergeben sich sog. Quantisierungsfehler, die maximal ½ Least Significant Bit (LSB) groß sein können. D.h., bei der Wiedergabe der Digitaldateien, werden einige Messpunkte etwas lauter wiedergegeben als es dem Original entspricht und andere etwas leiser. Eine Erhöhung der Raster-Anzahl (d.h., der Bittiefe) mindert das Problem, da es die Quantisierungsintervalle reduziert, kann es aber nie ganz beseitigen. Jedes extra Bit verdoppelt die Anzahl an Quantisierungsintervallen: 16Bit hat 216=65.536 Intervalle oder Lautstärkeabstufungen, 17Bit hat 217=131.072 Intervalle. Entsprechend werden mit jeden extra Bit die Größe der Intervalle und damit die Quantisierungsfehler halbiert, was sich nicht zuletzt auch in einer Reduzierung des Rauschabstands um 6dB pro extra Bit bemerkbar macht.

Graphik 3: Quantisierungsfehler
Bei hohen Signalpegeln wird sich die Größe des Quantisierungsfehlers mit gleicher Wahrscheinlichkeit zwischen den Grenzen ± ½LSB verteilen, so dass die Quantisierungsfehler zufällig verteilt sind und damit wie unkorreliertes weißes Rauschen – also wenig störend – wirken. Zu niedrigen Signalpegeln hin werden sie im Verhältnis zum quantisierten Signal allerdings sehr groß und hören auf zufällig verteilt zu sein, so dass sie bei niedrigen Signalpegeln zu auffälligem und störendem „Granulatrauschen“ (eine Art nicht-lineare Verzerrung) führen. Während bei der „alten“ Analogtechnik Verzerrungen mit steigendem Aufnahmepegel zunahmen, ist es bei der Digitaltechnik genau umgekehrt: gerade kleine Pegel können zu unangenehmen hörbaren Verzerrungen führen. Um diese Artefakte unhörbar zu machen, führt man das sog. Dithering durch – man fügt dem analogen Signal vor der Quantisierung ein Rauschen mit bestimmten statistischen Eigenschaften zu, um die treppenstufenartige Übertragungsfunktion, die bei geringen Pegeln entsteht, zu glätten. Durch Zugabe von Dither-Rauschen nimmt der Quantisierungsfehler einen rauschartigen und signalunabhängigen Charakter an. Dithering hat die Aufgabe, den bei kleinen Pegeln auftretenden Quantisierungsfehler, der ein mit dem Musiksignal korreliertes verzerren darstellt, in ein zum Musiksignal unabhängiges weißes Rauschen zu transformieren. Dabei verdeckt das Dithering nicht die Quantisierungsfehler, sondern erlaubt dem ADC Amplituden kleiner als das Least Significant Bit (LSB) zu codieren. Als Folge, verhält sich das digitale Signal wie ein analoges – es wird nicht zunehmend verzerrt wenn es leiser wird, sondern bleibt originalgetreu und sauber, bis es unter dem Rauschteppich verschwindet.
Neben dem Quantisierungsfehler können sich bei der Quantisierung auch andere Fehler ergeben, z.B. Nullpunktfehler (Offset), Verstärkungsfehler (Gain Error), Nichtlinearitätsfehler, Stufungsfehler und das vieldiskutierte Taktzittern (Jitter – Schwankungen in der Periodendauer des Taktsignals), die zu einer Abweichung des rekonstruiertem Digitalsignal vom originalen Analogsignals führen.
III. Gehen beim Digitalisieren Informationen verloren?
Die unmittelbar sich aufdrängende Frage ist, ob beim Digitalisieren (Sampling & Quantisieren) nicht Informationen zwischen den Messpunkten verloren gehen, so dass die digitale Reproduktion des analogen Tonsignals inhärent unvollständig und damit minderwertig ist. Die Antwort ist – überraschender Weise – Nein. Zumindest bei der korrekten Anwendung des Abtasttheorems gehen keine Informationen verloren. Die aus den digitalen Daten rekonstruierte Wellenform entspricht exakt der ursprünglichen analogen Wellenform. Die Digitalisierung beeinflusst weder den Frequenzverlauf noch das Phasenverhalten.
Zwar ergibt sich aus der Menge an Messpunkten (rote Punkte in Graphik 4) eine Vielzahl alternativer möglicher Frequenzverläufen (z.B. gestrichelte Linie in der folgenden Graphik), die alle die Menge an Messpunkten vollständig abdecken. Allerdings haben alle außer einem eine höhere als die Nyquist-Frequenz. Durch einen Tiefpassfilter, der alle Frequenzen oberhalb der Nyquist-Frequenz herausfiltert, kann sicher gestellt werden, dass nur der Frequenzverlauf – aus allen möglichen Frequenzverläufen, die alle Messpunkte abdecken – übertragen wird, der exakt dem ursprünglichen analogen Frequenzverlauf entspricht.

Graphik 4: Alternative Frequenzverläufe für alle Messpunkte
In anderen Worten, da der ursprüngliche Frequenzverlauf der mit der höchstmöglichen Frequenz ist, der noch alle Punkte abdeckt, garantiert das Nyquist-Shannon-Abtasttheorems, das nach Anwendung des Rekonstruktionsfilters, der rekonstruierte Frequenzverlauf nicht vom originalen Frequenzverlauf abweichen kann.
Für das Beispiel des Red Book Standards heißt das, dass mit der dort verwendeten Abtastrate von 44,1 kHz theoretisch Tonsignale bis 22.050Hz verlustfrei digitalisiert werden können. Da das menschliche Gehör, maximal Töne von ca. 20Hz bis 20.000Hz wahrnehmen kann, sollte die Digitalisierung nach dem Red Book Standard zumindest, was die Abtastrate anbelangt, für alle Audioanwendungen ausreichend sein. Dass sie das am Ende in der Praxis nicht ganz ist, weil die im Konvertierungsprozess nötigen, verfügbaren Filter nicht hinreichend steilflankig (bei einer bestimmten Frequenz scharf abschneidend) sind, um im Bereich zwischen 20.000Hz und 22.050Hz das Signal hinreichend zu dämpfen ohne die Frequenzbereiche darunter zu beschädigen, werden wir weiter unten noch besprechen.
Das heißt allerdings nicht, dass das korrekte Digitalisieren ein verlustfreier Prozess ist. Denn die Wahl der Worttiefe ist willkürlich und jedenfalls verlustbehaftet. Einen kontinuierlichen Amplitudenverlauf kann ein quantisiertes Digitalsignal egal in welcher Worttiefe nicht verlustfrei reproduzieren. Allerdings gibt es ein Punkt, ab dem psychoakustisch, keine Unterschiede in der Dynamikabstufung mehr wahrnehmbar sind. Wo genau dieser Punkt liegt, ist Gegenstand verschiedener Forschungsbemühungen. Generell geht man davon aus, dass das Amplitudenauflösungsvermögen des menschlichen Gehörs über 1 Mio. Abstufungen zulässt, so dass es noch Lautstärkeunterschiede von 0,0001dB unterscheiden kann, was in etwa der Größenordnung eines 20-22Bit Digital-Systems entsprechen würde.
IV. Nyquist-Shannon-Abtasttheorem und Aliasing
Dem Nyquist-Shannon-Abtasttheorem folgend kann eine vollständige (d.h. verlustfreie) Abbildung eines bandbegrenzten Signals bei zeitlich konstanter Abtastrate mit der oberen Grenzfrequenz fN (auch Nyquist-Frequenz genannt) durch eine zumindest doppelt so hohe Abtastrate fS erreicht werden:
f S > 2xfN
Ein periodisches, diskretes Abtasten des Signals im Zeitbereich hat im Frequenzbereich ein ebenso periodisches, diskretes Spektrum zur Folge. Es entstehen sog. Aliasing-Effekte, d.s. Ultraschall-Spiegelungen des ursprünglichen analogen Signals bei Vielfachen der Abtastrate (fS) und Nutzfrequenz (fN):

Graphik 5: Aliasingeffekte einer Nutzfrequenz fout
Wird das Nyquist-Shannon-Abtasttheorem verletzt, indem Komponenten der Nutzfrequenzen höher als fS/2 mit abgetastet werden, kommt es zu sog. Aliasingfehlern. D.s. Überlagerungen der Spiegelspektren mit der Folge, dass auch im hörbaren Bereich Störsignale sich aus der nächsthöheren Spiegelung überlagern und sich als Störungen und Verzerrungen bemerkbar machen, so dass das rekonstruierte Tonsignal nicht mehr dem ursprünglichen analogen Signal entspricht.

Graphik 6: Aliasingfehler, wenn fN> ½fS
Deshalb ist die Bedingung der Bandbegrenzung wichtig. Mittels eines analogen Tiefpassfilters (Filter, der alle Frequenzen unterhalb durchlässt und alle darüber blockiert) zur Beschränkung der Eingangsfrequenz fN wird das Signal bandbegrenzt, so dass Abtastfehler vermieden werden. Ein derartiges Filter sollte möglichst steilflankig sein und eine hohe Dämpfung aufweisen, z.B. muss beim Red-Book-Standard das Filter zwischen 20,0kHz und 22,05kHz um -96dB fallen – was sich selbst mit aufwändigsten Filtern höherer (achter oder höherer) Ordnung nur schwer erzielen lässt. Dennoch werden mit analogen Filtern zwangsläufig Teile des Signals unter der Nyquist-Frequenz gedämpft und Teile über der Nyquist-Frequenz nicht vollständig eliminiert:
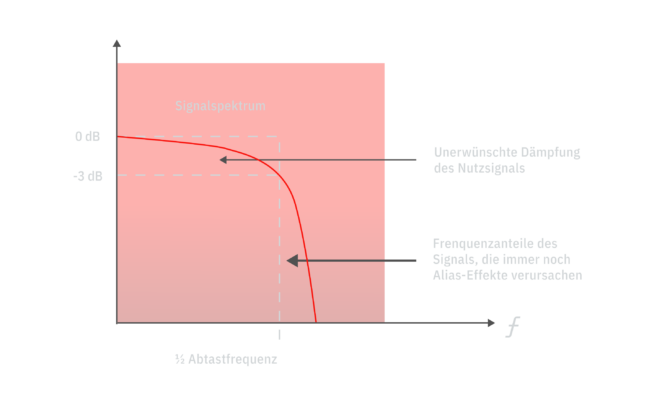
Graphik 7: Unzulänglichkeit analoger Filter
Die genaue Wahl der Grenzfrequenz für den Filter stellt daher in der Praxis einen Kompromiss zwischen der Erhaltung des Nutzsignals und der Eliminierung von Aliasfehlern dar. Obendrein verursacht das Filter eine Reihe von Verzerrungen und Problemen im Nutzsignal (z.B. Ringing, Group Delay, Phasenverzerrungen etc.), so dass heutzutage im Allgemeinen statt der analogen Anti-Alisingfilter das Eingangssignal mit einem Vielfachen der Abtastfrequenz abgetastet (Oversampling) und anschließend digital gefiltert wird. Dabei entsteht ein größerer Sicherheitsabstand zwischen dem Nutzfrequenzband und dem Alias-Spektrum, was die Anforderungen an das Filter deutlich reduziert. Außerdem sind Filter im digitalen Bereich zwar im Design mathematisch anspruchsvoll, aber leicht zu realisieren.
V. Oversampling
In der digitalen Signalverarbeitung spricht man von Oversampling, wenn ein Signal per Abtastratenkonvertierung mit einer höheren Abtastrate (meist ganzzahlige Vielfache) abgetastet wird, als für die Darstellung der Signalbandbreite (gem. Nyquist-Shannon-Theorem) eigentlich benötigt wird. Wie dargelegt, ist es technisch kaum machbar, die Anforderungen an Anti-Aliasingfilter im analogen Bereich zu erfüllen. Im digitalen Bereich dagegen, geht das mit FIR-Filtern (Finite Impulse Response-Filter) viel einfacher, die obendrein auch viel weniger problematisch bzgl. Phasenverhalten und Gruppenlaufzeiten sind als entsprechende analoge Filter. Durch Erhöhung der Abtastrate wird erreicht, dass die Spiegelspektren erst erheblich höher einsetzen, somit deutlich mehr Frequenzbandbreite zur Anwendung des Filters verfügbar ist und damit weichere Tiefpässe (zweiter oder dritter Ordnung) als Anti-Aliasing-Filter eingesetzt werden konnten. Oversampling erlaubt es somit, die Filterung des Nutzsignals vom analogen in den digitalen Bereich zu verschieben und damit den Geräuschabstand zu verbessern sowie Aliasing- und Phasen-Verzerrungen zu vermeiden. Die Filterung erfolgt mit einem leichter realisierbaren Digitalfilter; am Konverter-Ausgang ist dann nur noch ein relativ einfaches analoges Rekonstruktionsfilter notwendig.

Graphik 8: Oversampling erweitert den Arbeitsbereich der Antialiasingfilter
Allerdings ist die Realisierung eines digitalen Anti-Aliasingfilters als Voraussetzung für die Digitalisierung konzeptionell herausfordernd, muss das Signal doch vorher bereits digitalisiert sein. Die Lösung ist eine clevere Ingenieursleistung mithilfe des Oversamplings:
Nehmen wir als Beispiel 2-faches Oversampling:
Beim 2-fachen Oversampling wird auf der Analog-Digital-Wandlungsseite das analoge Tonsignal zuerst durch einen milden analogen Tiefpassfilter auf z.B. 1,5 fS begrenzt. Das ermöglicht eine Ausweitung des Filterbereiches auf 0,5fS – 1,5fS. Das entspricht am Beispiel des Red-Book-Standards einer Ausweitung des Frequenzbandes zum Filtern um das 20-fache von 2,05kHz auf 44,1kHz. Anschließend wird das Signal mit der doppelten Abtastrate quantifiziert und durch einen digitalen Tiefpassfilter mit anschließender Dezimierung der Abtaststellen durch 2-faches Undersampling zum digitalen Signal ohne Aliasingfehler mit der gewünschten Abtastrate fS konvertiert.
Beim 2-fachen Oversampling wird auf der Digital-Analog-Wandlungsseite das digitale Signal per Abtastratenkonvertierung und digitalem Tiefpassfilter verdoppelt, bevor es ins Analoge konvertiert wird und abschließend mit einem analogen Tiefpassfilter gem. dem Nyquist-Shannon-Theorem wieder fehlerfrei rekonstruiert wird.
Der Multiplikator des Oversamplings kann von 2, 4 oder 8 bis zu 64 oder 128 (5,6 MHz Abtastrate) bei DSD-Produktionen reichen.
Ein positiver Nebeneffekt ist, dass durch Oversampling der Störabstand verbessert wird. Das zuvor erwähnte breitbandige, vom Eingangssignal unkorrelierte Quantisierungsrauschen bei höheren Pegeln verteilt sich auf ein breiteres Spektrum bis zur neuen Nyquist-Frequenz kfS/2. Demzufolge existiert weniger Störleistung im nutzbaren Audioband. Innerhalb der gleichen Bandbreite verringert sich der Störpegel bei jeder Verdoppelung der Samplingfrequenz um 3dB.

Graphik 9: Verschiebung des Quantisierungsrauschens durch Oversampling
Die digitalen Filter führen allerdings zu einem neuen Phänomen: dem Pre-Ringing, bei dem die Impulsantwort, neben dem Nachschwingen (das es auch bei analogen Filtern auftritt) auch ein unnatürliches Vor-Schwingen (Pre-Ringing) vor dem Eintritt des eigentlichen Signals aufweist, so dass das Filter das Signal über die Zeit “verschmiert”. In den nachfolgenden Graphiken 9 & 10 wird der ursprüngliche Impuls mit einer Breite von exakt 1 Sample durch den Filter über viele Samples zeitlich verschmiert. Dieses Phänomen wird hauptsächlich für die teilweise unnatürliche Klangqualität von Digitalaufnahmen (harte Klangtexturen, flache Räumlichkeit, hohe Frequenzen, die gleichzeitig eng und brillant klingen etc.) verantwortlich gemacht:

Graphik 10: Originaler Impuls von 1 Sample
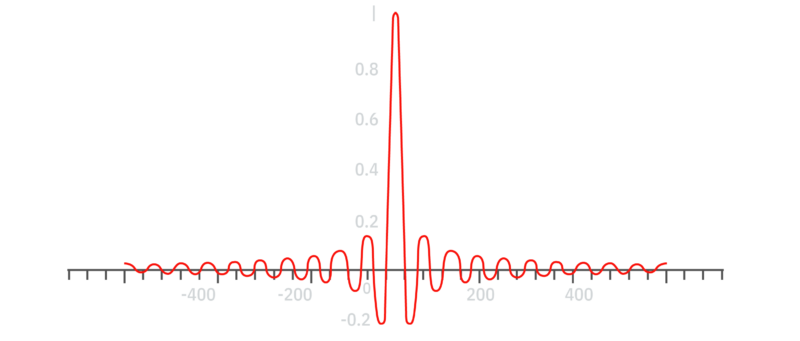
Graphik 11: Impuls nach Anwendung linearphasigen Filters
Oversampling führt, nebenbei bemerkt, nicht zu höheren Datenraten und höherem Speicherplatzverbrauch, da dieses Verfahren beim Auslesen und nicht beim Schreiben von Daten Anwendung stattfindet.Das Pre-Ringing entsteht bei den steilflankigen Anti-Aliasing-Filtern der AD-Konverter ebenso, wie bei den üblichen steilflankigen, linearphasigen Rekonstruktionsfiltern der DA-Konvertierung primär bei niedrige Abtastraten, wie 44,1kHz oder 48,0kHz. Inwieweit das Filter-Ringing tatsächlich die Wiedergabequalität beeinflusst ist jedoch unklar. Das Ringing tritt im Allgemeinen zwischen dem Passband und dem Stopband eines Filters auf, im Beispiel einer CD, also zwischen 20kHz und 22,05kHz, bei höheren Sampleraten bei entsprechend höheren Frequenzen. Das Pre-Ringing, das bei linearphasigen Filtern am ausgeprägtesten ist, kann durch alternative Filtertopologien (Minimum-Phase, Apodizing etc.) gemildert werden. Allerdings stellen diese alternativen Filter immer nur ein Kompromiss dar, da sie Nachteile in anderen Bereichen mit sich bringen, wie Phasenverzerrungen oder Höhenabfall. Weitgehend vermeiden lässt sich das Phänomen durch höhere Abtastraten und sanftere Filterverläufe.
VI. Digitalisierungsprozess (Sigma-Delta-Verfahren)
Mit dem Grundlagenwissen können wir uns nun den Prozessschritten bei der Digitalisierung anschauen:
Die technische Realisierung von Analog-Digital-Wandlern findet in der heutigen digitalen Audiotechnik hauptsächlich durch das Sigma-Delta-Verfahren statt. Die Idee des Oversamplings weiterführend, wird mit 64-facher Standard-Abtastfrequenz gearbeitet (64×44,1 kHz = 2,8224 MHz), allerdings ursprünglich nur mit einem Bit Wortbreite. Ein Sigma-Delta-Wandler (ΔΣ-Wandler, s. Grafik Nr.11) besteht grundsätzlich aus zwei Stufen, einem analogen Modulator und einem digitalen Filter. Der analoge Modulator setzt sich prinzipiell zusammen aus einem in Reihe geschalteten Eingangsdifferenzverstärker, einem Integrierer (Σ) und einem Komparator (Δ), der als 1-Bit-Quantisierer fungiert, und einem Ein-Bit-D/A-Wandler im Gegenkopplungszweig. Mit Hilfe des darauffolgenden, die Abtastrate dezimierenden, digitalen FIR-Filters, das prinzipiell wie ein mittelwertbildender Akkumulator (für die Abtastwerte) funktioniert, wird das digitale Ausgangswort mit der gewünschten Samplefrequenz und Wortbreite erzeugt.
Die grundsätzliche Funktionsweise lässt sich am besten anhand eines Sigma-Delta-Wandlers erster Ordnung zeigen (die Ordnung wird bestimmt durch die Zahl der Tiefpässe oder Integrierer vor dem Komparator):

Grafik 12: Prinzipieller Aufbau eines Sigma-Delta-Wandlers.
Durch den Eingangsdifferenzverstärker wird vom Eingangssignal das gegengekoppelte Ausgangssignal des 1-Bit-D/A-Wandlers subtrahiert, zu messen am Punkt V1. Dieses wird im Integrierglied zu dessen vorherigem Ausgangssignal hinzuaddiert (Messpunkt V2) und anschließend im Komparator mit einer Spannung von 0V verglichen. Ist V2 größer als 0V nimmt er am Ausgang ( = V3) einen Spannungswert von +1V an, sollte er kleiner als 0V sein, legt er den Ausgang auf –1V. Im Gegenkopplungszweig schaltet der getaktete Ein-Bit-D/A-Wandler entsprechend des Messpunktes V3 auf + bzw. –1 Volt und gibt diesen Wert an den Eingangs-Differenzverstärker weiter, wo er wiederum vom nun anliegenden eventuell veränderten Eingangssignal VIn abgezogen wird. Dieser Zyklus wiederholt sich pro Abtasttakt.
Das am Ausgang des Modulators eines einfachen Ein-Bit-ΔΣ-Wandlers anliegende Signal enthält allerdings einen extrem hohen Anteil an Quantisierungsrauschen. Der resultierende Signal/Rauschabstand wäre so schlecht (6dB) – obwohl sich die Rauschleistung bis zur Nyquistfrequenz bei 1,4112 MHz verteilt – dass man den gewünschten Dynamikumfang nur durch spektrale Formung im sogenannte Noise-Shaping-Verfahren erreichen kann. Hierbei wird das statistisch gesehen weiße Rauschen im Spektrum so verschoben, dass davon möglichst wenig auf das Audioband (20Hz – 20kHz) entfällt. Zwar verringert sich die Summe des gesamten Rauschens nicht, sondern die im Audioband reduzierte Rauschmenge erhöht die Rauschmenge im übrigen Bereich. Noise-Shaping wird erreicht, indem die Quantisierungsfehler, die zum Quantisierungsrauschen führen, durch ein Feedback-Loop aus dem 1Bit-D/A-Wandler mit einer zeitlichen Verschiebung von 1 Sample und negativem Vorzeichen in den Differenzverstärker zurückgespeist werden. Da jedes Feedback-Loop als Filter fungiert, kann mit dem Zurückspeisen des Fehlersignals der Fehler selber gefiltert werden. Die Verformung des Quantisierungsrauschens erfolgt bereits im Integrierglied, somit also schon im analogen Bereich. Wenn man den Integrierer als analogen Tiefpassfilter realisiert, ergibt sich ein Ausgangssignal, das aus der Summe des tiefpassgefilterten Eingangssignals und des hochpassgefilterten Rauschens besteht. Somit erfüllt er einerseits die Anti-Aliasing-Filterung, andererseits aber auch die spektrale Verformung des Quantisierungsrauschens.
Das nachfolgende digitale Dezimierungsfilter verrichtet ebenso wie das Integrierglied zwei Aufgaben: zum einen wird das Quantisierungsrauschen mitsamt aller Audioanteile oberhalb der halben Samplingfrequenz herausgefiltert, so dass eine Unterabtastung auf die gewünschte Samplingfrequenz möglich ist (Abtasttheorem), zum anderen dient das FIR-Filter zur Erzeugung der erforderlichen Wortbreite des Ausgangssignals. Dies geschieht durch das Zusammenfassen mehrerer verzögerter 1-Bit-Samples zu einem n -Bit-Sample. Die dadurch erzielbare Wortbreite ist nicht von der Dynamik des Sigma-Delta-Modulators abhängig, sondern von der Filterfunktion
Auf der D/A-Seite kommt wiederum der ΔΣ-Wandler zum Einsatz. Hierfür wird das Audiosignal zuerst auf üblicherweise das 8-fache der Standard-Abtastrate überabgetastet (Oversampling mit Hilfe eines Interpolationsfilters), nach dem ΔΣ-Wandler steht anschließend wieder das Ein-Bit-Stream-Signal zur Verfügung. Von einem internen Switched-Capacitor-Filter (S.C.F. lowpass) wird es abschließend analog vorgefiltert.
Zusammenfassend schaut der PCM-A/D- und -D/A-Wandlungsprozess und Verwendung des Sigma-Delta-Verfahrens folgendermaßen aus, wobei die aus Einfachheitsgründen oben beschriebene Verwendung eines 1Bit-Wandlers, wie heute üblich, durch einen Multibit-Wandler (zumeist 4 oder 8Bit) ersetzt wurde:

Graphik 13: Moderner PCM AD- und DA-Wandlungsprozess
Zunächst findet unter Verwendung eines Sigma-Delta-Wandlers die A/D-Konvertierung mit hoher Abtastrate statt. Anschließend kann durch Dezimierung mit einem digitalen FIR-Filter die gewünschte Quantisierung bei entsprechender Samplingfrequenz erreicht werden. Nach dem Aufzeichnungsvorgang ist für die D/A-Rückkonvertierung zunächst eine Interpolation (Oversampling) mit recht steilflankigen Filtern und erneute Sigma-Delta-Wandlung erforderlich, bevor das Signal durch Tiefpassfiltering wieder als analoges Ausgangssignal zur Verfügung steht.
B. DIRECT-STREAM-DIGITAL (DSD)
Hier setzt nun die Idee der Direct-Stream-Digital-Technologie (DSD) an, die Ende der 90er Jahre von Philips für Archivierungszwecke entwickelt wurde: Ließe man das Dezimationsfilter, das Oversamplingfilter und den Sigma-Delta-Modulator einfach weg, und würde das Ein-Bit-Datensignal geradewegs aufzeichnen sowie direkt zu den analogen Tiefpässen auf der D/A-Wandler-Seite schicken, könnte man nicht nur einige Bauteile einsparen, sondern v.a. die steilflankigen Anti-Aliasing-Filter (und das assoziierte Pre-Ringing) vermeiden. Auch wenn die Speicherung des ungefilterten DSD-Datenstroms mehr Kanalkapazitäten als notwendig erfordert, bedeutet der Wegfall natürlich eine sichtliche Vereinfachung. Im Endeffekt entsteht eine Pulse Density Modulation (PDM), die nicht mehr die Amplitude des Signals quantifiziert, sondern nur noch die Differenz der Amplitude zum vorherigen Sample:

Graphik 14: Moderner 1Bit DSD AD- und DA-Wandlungsprozess
Grundsätzlich gilt im Audiobereich, dass je einfacher eine elektrische Schaltung ist und je weniger in das zu transportierende Analogsignal eingegriffen wird, desto höher ist die Wiedergabetreue des Signals, so dass ceteris paribus, einfachere Systeme vorzuziehen sind.
Durch die technische Weiterentwicklung der A/D- und D/A-Konverter als Multi-Bit-Wandler wird dieser scheinbare Vorteil der DSD-Technik wieder relativiert. Den Vorteilen der preiswerten Fertigung und einer sehr guten Linearität von Sigma-Delta-Wandlern steht der deutlich geringere Dynamikumfang sowohl auf A/D- als auch auf D/A-Seite gegenüber. Der Wunsch nach einer Erhöhung des Signal-Rauschabstandes konnte nur durch variierte Wandler erfüllt werden: es kamen schnelle 4- oder 5-Bit-Konverter statt der einfachen Komparatoren zum Einsatz, wodurch das notwendige Noise-Shaping weniger stark ausgelegt werden konnte. Um differentielle Nichtlinearitäten möglichst zu vermeiden, werden in den IC’s mehrere dieser Wandler eingesetzt, die das Signal jeweils per Zufall erhalten. Der Fehler, der sich aus der Nichtlinearität eines einzigen Wandlers ergibt, wird geglättet und macht sich als Rauschen bemerkbar.
Daraus ergibt sich, dass das bei DSD erforderliche Ein-Bit-Signal im Signalfluss heutiger Digitalproduktionen nun gar nicht mehr auftaucht, da als natives Format nach dem Sigma-Delta-Modulator jetzt ein Multi-Bit-Signal zur Verfügung steht. Damit aus dem (bereits digitalisierten) Ausgangssignal des Modulators das Ein-Bit-Signal gewonnen werden kann, ist ein nachgeschalteter digitaler Ein-Bit-Requantisierer erforderlich. Diese notwendige Stufe beinhaltet natürlich wiederum das Hinzufügen von zusätzlichen Verzerrungen und zusätzlichem Rauschen. D/A-seitig ist zwar die Berechnung des 4- bis 5-bittigen Modulator-Eingangswortes durch Tiefpassfilterung nötig, dies ist jedoch verzerrungsfrei möglich. Die digitale Vorfilterung ist sogar recht günstig, da hier bereits hochfrequente Störleistung beseitigt wird.
Somit ergibt sich folgende Prozessschematik für heutzutage übliche DSD-Aufzeichnung mit Hilfe mehrbittiger Sigma-Delta-Wandler:

Graphik 15: Moderner DSD AD- und DA-Wandlungsprozess
© Alexej C. Ogorek
Quellen:
- Ken C. Pohlmann: “Principles of Digital Audio”, 6th Edition, McGraw-Hill 2011
- HUGH ROBJOHNS: ” All About Digital Audio”, Sound-On-Sound, May 1998
- Dominik Blech, Min-Chi Yang: “Untersuchung zur auditiven Differenzierbarkeit digitaler Aufzeichnungsverfahren”, Hochschule für Musik Detmold, Erich-Thienhaus-Institut 2004

